作者:林淑芬 / 臺灣大學計算機及資訊網路中心教學研究組程式設計師
R軟體提供了眾多的套件,往往讓初學者無所適從,因此在這裡我們將以一個R內建的鳶尾花資料集為例,說明整個分析處理過程,包括敘述統計、繪圖功能、常態性檢定、雙樣本均數檢定、變異數分析、迴歸分析、決策樹資料探勘等分析應用,讓初學R軟體的人可以很快地掌握整個統計分析的處理過程。
本文以一個鳶尾花資料集為例,說明利用R進行分析的過程。初學者可以利用這個R內建的資料集,了解、熟習敘述統計、繪圖、以及各項分析與探勘的功能,對於未來真實案例的應用會有很大的幫助。
前言
R軟體提供了數量龐大的套件,往往讓初學者無所適從,因此在這裡我們將以一個R內建的鳶尾花資料集為例,說明整個分析處理過程,包括敘述統計、繪圖功能、常態性檢定、雙樣本均數檢定、變異數分析、迴歸分析、決策樹資料探勘等分析應用,讓初學R軟體的人可以很快地掌握整個統計分析的處理過程。
一. 敘述統計
這個R內建的鳶尾花(iris)資料集是非常著名的生物資訊資料集之一,取自美國加州大學歐文分校的機械學習資料庫http://archive.ics.uci.edu/ml/datasets/Iris,資料的筆數為150筆,共有五個欄位:
1. 花萼長度(Sepal Length):計算單位是公分。
2. 花萼寬度(Sepal Width):計算單位是公分。
3. 花瓣長度(Petal Length) :計算單位是公分。
4. 花瓣寬度(Petal Width):計算單位是公分。
5. 類別(Class):可分為Setosa,Versicolor和Virginica三個品種。
可先使用head和tail函數查看資iris料集的前5筆或後幾筆資料,順便檢視資料欄位名稱,前4個欄位為數值型態,第5個欄位為類別型態。
>head(iris,5)
接著以mean函數算出Sepal.Length的平均值:
>mean(iris$Sepal.Length)
若是只想取到小數第二位,則可利用round函數:
>round(mean(iris$Sepal.Length),2)
由於某些資料檔名稱或變數名稱很長,像iris$Sepal.Length這樣的寫法很麻煩,這時我們可以先使用attach函數,建立與iris資料集的連結,之後就可直接使用變數名稱來操作:
>attach(iris)
>round(mean(Sepal.Length),2)
>summary(iris)
最後以summary產生基本敘述統計資料,包括數值資料的平均數、中位數、最大最小值、四分位數以及類別資料的次數。其他如變異數、標準差可使用var()、sd()函數。
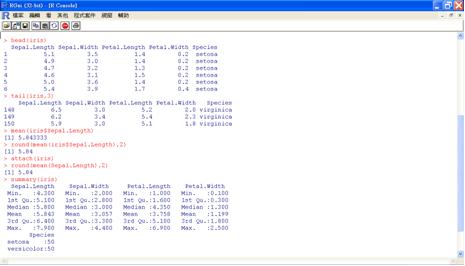
圖一 iris的基本敘述統計
二. 繪圖功能
plot函數可依參數的性質畫出不同的X-Y散佈圖、長條圖、盒狀圖、散佈圖矩陣:
>plot(Sepal.Length,Sepal.Width) 散佈圖
>plot(Species) 長條圖
>plot(Species,Sepal.Length) 盒狀圖
>plot(iris) 散佈圖矩陣
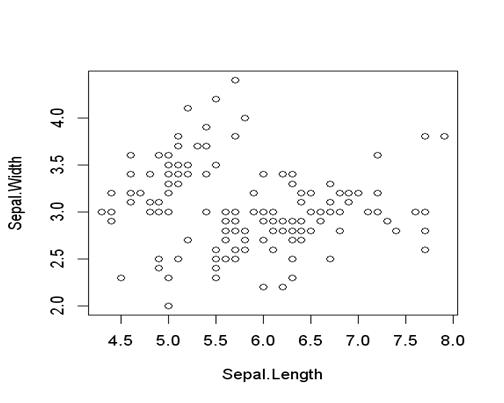
圖二 Sepal.Length和Sepal.Width散佈圖
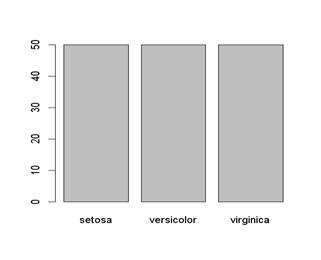
圖三 Species長條圖
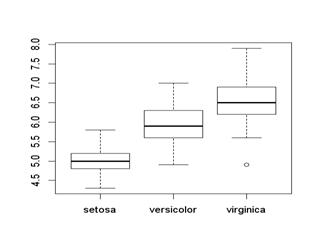
圖四 Sepal.Length對Speices盒狀圖(四分位圖)
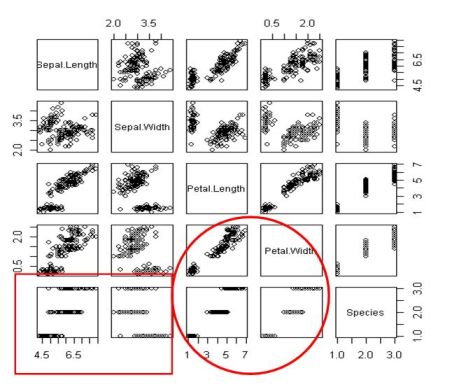
圖五 散佈圖矩陣
從上面的散佈圖矩陣的圈圈我們可以發現Petal.Length和Petal.Width之間存有線性關係,都可區分第1和第2個鳶尾花類別,即Setosa和Versicolor類別,而從方形框框中可看到第2和第3個鳶尾花類別,即Versicolor和Virginica的Sepal.Length和Sepal.Width分佈相近。
另外我們可以在plot畫好的圖形上,利用points和 legend指令加上附加圖形,產生三種不同圖樣顏色鳶尾花類別的Sepal.Length和Petal.Length分布圖:
>attach(iris)
>plot(Sepal.Length[Species=="setosa"],Petal.Length[Species=="setosa"], pch=1 ,col="black", xlim=c(4,8), ylim= c(0,8), main="classified scatter plot", xlab= "SLen", ylab= "PLen")
>points(Sepal.Length[Species=="virginica"], Petal.Length[Species== "virginica"],pch=3,col="green")
>points(Sepal.Length[Species=="versicolor"], Petal.Length[Species== "versicolor"],pch=2,col="red")
>legend(4,8,legend=c("setosa","versicolor","virginica"), col=c(1,2,3), pch=c(1,2,3))
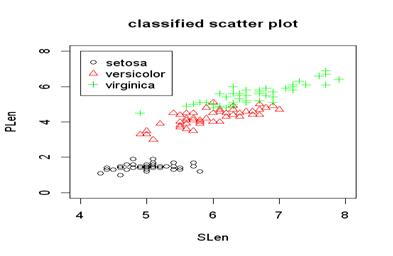
圖六 三種不同圖樣顏色的鳶尾花類別分布圖
三. 常態性檢定
如果我們想知道iris花瓣和花萼的長度和寬度這4項數值資料是否符合常態分配,則可使用常態機率圖或常態性檢定來檢查,以qqnorm函數畫出常態機率圖,再使用qqline畫出最佳斜線,至於常態性檢定則可使用R基本套組stats的shapiro.test函數進行Shapiro-Wilk檢定,或套組nortest的ad.test函數進行Anderson-Darling檢定,這裡就以Sepal.Length為例來說明:
attach(iris)
shapiro.test(Sepal.Length)
library(nortest)
ad.test(Sepal.Length)
qqnorm(Sepal.Length)
qqline(Sepal.Length,col="red")
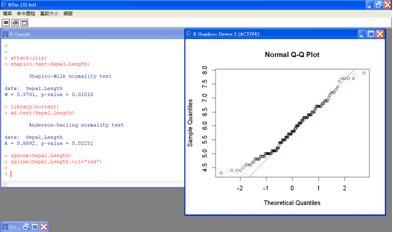
圖七 Sepal.Length常態機率圖和常態性檢定
從檢定結果可看出P值都是顯著的,得要棄卻Sepal.Length呈常態分配的虛無假設,所以我們想再畫出Sepal.Length的直方圖和常態曲線看看:
hist(Sepal.Length,breaks=seq(4.0,8.0,0.25),prob=TRUE)
curve(dnorm(x,mean(Sepal.Length),sd(Sepal.Length)),4.0,8.0,add=TRUE, col="red")
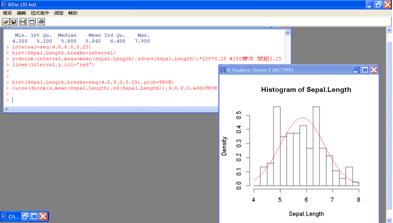
圖八 Sepal.Length直方圖和常態曲線
四. 雙樣本均數檢定
從圖五的散佈圖矩陣我們可以發現花瓣寬度Petal.Width可區分第1和第2個鳶尾花類別,即Setosa和Versicolor類別。因而我們想以t.test函數進行兩組獨立樣本t檢定,比較這兩個類別Petal.Width的平均數是否有顯著差異。
首先必須整理iris的資料,雖然iris是R的內建資料,但在分析問題時我們必須注意將資料整理成R可以分析的格式。再以var.test函數進行兩組變異數相同與否的F檢定。若變異數相同,則執行t.test時設定var.equal=TRUE,若變異數不相同,則設定var.equal= FALSE或省略。
先以xtabs函數作次數分配表,確定品種變數的名稱和筆數。再以第一種格式將品種setosa切成一個檔,versicolor切成一個檔,然後以這兩個向量去作檢定:
xtabs(~Species)
setosa=subset(iris,Species=="setosa")
versicolor=subset(iris,Species=="versicolor")
var.test(setosa$Petal.Width, versicolor$Petal.Width)
t.test(setosa$Petal.Width, versicolor$Petal.Width, var.equal=FALSE)
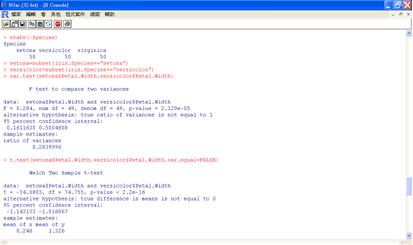
圖九 第一種資料格式的F檢定和t檢定
第二種格式是將品種virginica刪除,成為只剩下setosa和versicolor100筆的iris2資料集,以formula形式檢定:
iris2=subset(iris,Species!="virginica")
var.test(iris2$Petal.Width ~ iris2$Species)
t.test(iris2$Petal.Width ~ iris2$Species,var.equal=FALSE, conf=0.95)
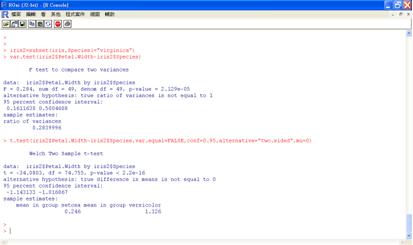
圖十 第二種資料格式的F檢定和t檢定
五. 變異數分析
如果t檢定是用於兩組資料比較平均數差異時;而比較三組以上的平均數是否相等時,就須使用到變異數分析(ANOVA,Analysis of Vairance)。如我們想檢定iris三個品種的Petal.Width平均數是否有顯著差異?
H0:μSetosa=μVersicolor=μVirginica
H1:至少有一種平均數和其他品種不相等
從下圖的ANOVA表我們得知檢定結果顯著,不同品種間的花瓣寬度有顯著不同,而summary的R²或adjusted R²可看出因子的解釋能力。Cofficient的Intercept是reference group(此為Setosa的平均),第二行是估計Versicolor平均和Setosa平均的差,第三行則是估計Virginica和Setosa平均的差,這兩個t檢定的結果都顯著。
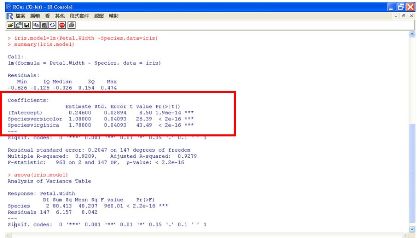
圖十一 單因子變異數分析
但如果我們還要比較Versicolor和Virginica平均的差呢? R軟體提供數種多重比較的工具,無論比較的組數多寡,都是一次性檢定。這裡我們使用multcomp套件的glht函數,進行多重均數比較,並畫出多重比較圖形:
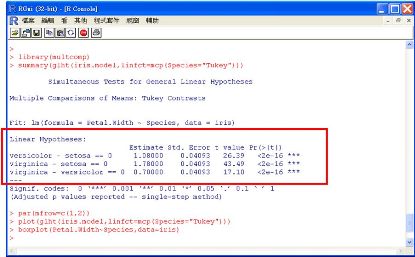
圖十二 多重比較
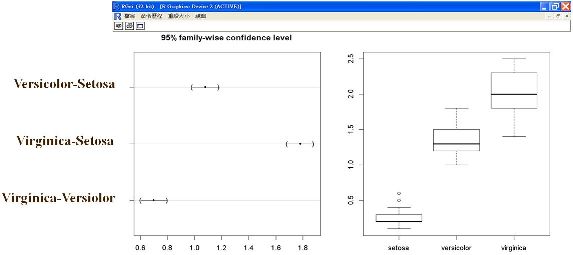
圖十三 多重比較圖形
我們還可以使用laercio套件的LTukey和LDuncan函數,進行Tukey和Duncan多重比較分組,同為a組或b組表示沒有顯著差異,分別歸類到a組或b組則表示有顯著差異:
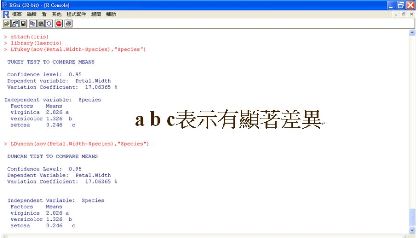
圖十四 多重比較分組
六. 迴歸分析
迴歸分析是以一個或一組自變數(解釋變數、預測變項,Xi),來預測一個數值性的因變數(依變數、應變數、被預測變項,Y)。若只有一個自變數稱為簡單迴歸;若使用一組自變數則稱為多元迴歸或複迴歸。主要函數為lm (Linear Model):
model=lm(Y~X1+X2+…+Xk, data=…)
在這裡我們以Sepal.Length為依變數Y,以Sepal.Width、Petal.Length、Petal.Width為自變數進行迴歸分析:
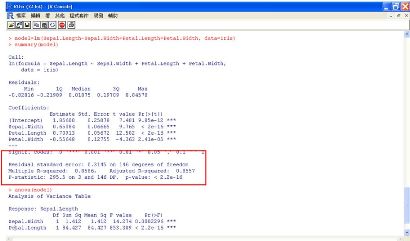
圖十五 迴歸分析
此模型的3個自變數和常數項t檢定都顯著,因而模型為:
Sepal.Length = 0.65084xSepal.Width + 0.70913xPetal.Length - 0.55648xPetal.Width + 1.85600
判定係數(R平方)為0.8586,調整後的R平方為0.8557相當具解釋力,判定係數愈大代表可解釋的部份愈大。殘差的標準差為0.3145(Root MSE,又稱預測標準誤)越小越好。F檢定和t檢定的p值也是越小越好。
七. 決策樹資料探勘
決策樹(Decision Tree)是常用的資料探勘技術,可視為迴歸分析的擴充。決策樹可用於分類預測,此類決策樹稱為分類樹(Classification Tree)。這裡要舉例的分類迴歸樹(CART, Classification and Regression Tree)是由Brieman在1984年提出,他並於2001年提出Random Forest決策樹。在這裡我們先將資料隨機分為90%訓練組,10%測試組,再使用rpart套組的rpart函數和tree套組的tree函數來建構CART決策樹:
n=0.1*nrow(iris)
test.index=sample(1:nrow(iris),n)
iris.train=iris[-test.index,]
iris.test=iris[test.index,]
library(tree)
iris.tree=tree(Species~ . ,data=iris.train)
iris.tree
plot(iris.tree)
text(iris.tree)
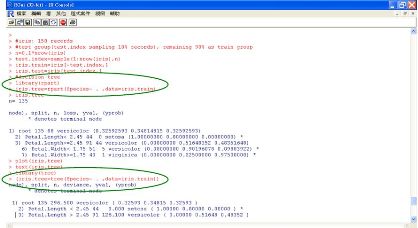
圖十六 和rpart函數的分類決策樹執行結果
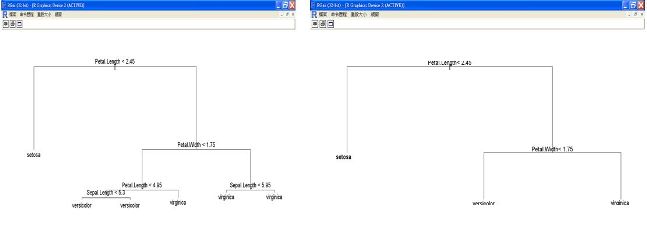
圖十七 tree和rpart函數的樹狀圖
以上是tree和rpart函數的分類樹狀圖,由於是不同的演算法,所以決策樹的切割條件也不盡相同,兩者的混淆矩陣與預測正確率也不盡相同。以下是tree的混淆矩陣與預測正確率分析,我們可以看到90%訓練組的資料,正確率為97%。而再執行其餘的10%測試組資料時,正確率竟高達100%。
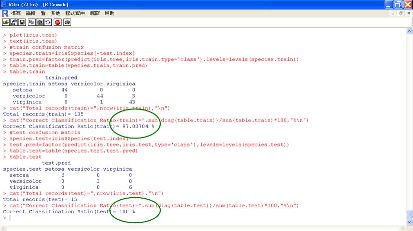
圖十八 tree的混淆矩陣與預測正確率
最後我們再以Brieman於2001年提出的Random Forest決策樹,利用iris資料的花瓣和花萼的長度和寬度,來預測鳶尾花的種類。R軟體也提供randomForest套組的randomForest函數來建立模型,同樣先將資料隨機分為90%訓練組,10%測試組。
以下指令是使用randomForest套組的randomForest函數,使用90%訓練組資料來建構隨機森林決策樹以及產生混淆矩陣與預測正確率,接著使用10%測試組資料產生混淆矩陣與預測正確率:
#Random Forest
library(randomForest)
set.seed(777)
iris.rf=randomForest(Species ~ ., data=iris.train,importane=T,proximity=T)
print(iris.rf)
round(importance(iris.rf),2)
names(iris.rf)
(table.rf=iris.rf$confusion)
sum(diag(table.rf)/sum(table.rf))
#predict
(rf.pred=predict(iris.rf,newdata=iris.test))
(table.test=table(Species=species.test,Predicted=rf.pred))
sum(diag(table.test)/sum(table.test))
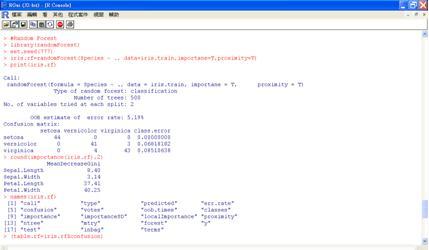
圖十九 隨機森林決策樹
從下圖的結果看到訓練組的資料,正確率為94.7%。而測試組資料,正確率竟高達100%。
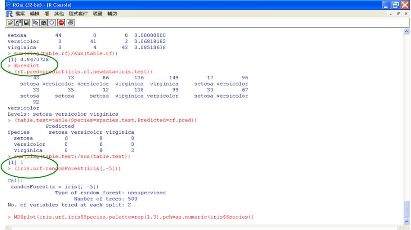
圖二十 隨機森林的混淆矩陣與預測正確率
此外,randomForest也可以處理沒有應變樹的資料,單純依據自變數作觀察值的分群。例如以下指令將Species變數移除後,利用花瓣和花萼的長度和寬度,來對150朵鳶尾花作分群,大致分為3大群不同的種類,通常稱之為集群分析(Clustering)。集群分析不需要事先定義好該如何分類,也不需要訓練組資料,而是靠資料自身的相似性集群在一起,最常使用在市場區隔的應用上。
(iris.urf=randomForest(iris[,-5]))
MDSplot(iris.urf,iris$Species,palette=rep(1,3),pch=as.numeric(iris$Species))
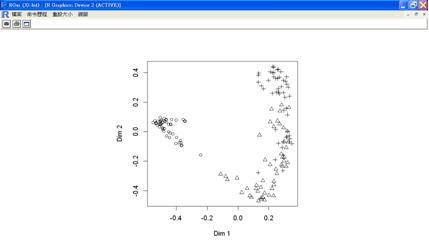
圖二十一 隨機森林的集群分析圖