計資中心電子報C&INC E-paper

作者：張晏瑞 / 中原大學 智慧運算與大數據碩士學位學程 助理教授

---

本篇延續前兩篇內容，示範如何在 Python／Qiskit 環境中實作一個最小可運作的「離散時間量子行走（DT‑QW）」並繪出行走後的機率分佈。讀者可直接將程式貼入 Google Colab（或 JupyterLab）執行，實際感受量子行走的干涉與快速擴散特性。

 

核心概念回顧

硬幣位元 (coin qubit) – 量子版的「擲硬幣」，決定下一步向左或向右。

條件位移 (conditional shift) – 依硬幣結果更新位置位元。

酉演化 – 不在每一步測量，使干涉得以累積並加速擴散。

完整流程：

1. 定義硬幣算符與條件位移算符；

2. 構建單步演化算服 $U=S(C\otimes I)$；

3. 反覆施行$U$以模擬多步行走；

4. 量測並視覺化位置機率分佈。

程式碼分成NumPy 純矩陣版（教學直觀）與Qiskit 量子電路版（貼近實機）兩段，讀者可依需求選用。透過實作，您將直觀體驗量子疊加與干涉如何改變隨機漫步的擴散行為。

1. NumPy 快速雛形（教學版）

用途：不依賴外部量子套件，快速驗證干涉造成的機率分佈差異。

環境：NumPy＋Matplotlib（Colab 預設即有）。

 

第一步設定了量子行走的基本參數：

• num_positions = 8：定義了一維空間中有8個可能的位置（標記為0到7）
• steps = 0：設定初始狀態，尚未進行任何步數的行走
• dim = 2 * num_positions：整個系統的希爾伯特空間維度，等於硬幣空間（2維）張量積位置空間（N維）

 

第二步量子算符定義：

• 硬幣算符 (Hadamard)：這定義了作用在硬幣上的Hadamard算符，它能將$|0⟩$和$|1⟩$態轉換為均勻疊加態，將$|0⟩$轉換為$\frac{(|0⟩+|1⟩)}{\sqrt{2}}$，將$|1⟩$轉換為$\frac{(|0⟩-|1⟩)}{\sqrt{2}}$，設定為複數型態以處理量子態的複數振幅。
• 條件位移算符：這定義了條件位移算符，根據硬幣狀態決定位置的移動方向：建立一個dim×dim的零矩陣作為位移算符，對每個位置p和硬幣狀態c進行迭代。若硬幣狀態為|0⟩，則向左移動一格，若硬幣狀態為|1⟩，則向右移動一格，矩陣中的1表示從源狀態到目標狀態的轉移。

第三步結合了硬幣和位移動作，形成完整的單步演化算符：

• np.kron(H, np.eye(num_positions, dtype=complex))：計算Hadamard算符與位置空間單位矩陣的張量積
• S @ ...：矩陣乘法，計算S與(H⊗I)的複合作用
• 這形成了量子行走的完整單步演化U

第四步初始狀態設定，這定義了量子行走的初始態：

• 使用整數除法計算中心位置（對於num_positions=8，中心為4）
• 創建長度為dim的零向量作為量子態
• 將中心位置的振幅設為1，表示行走者初始時100%位於中心位置
• 由於索引直接使用center_position，這表示初始硬幣狀態為$|0⟩$

第五步迭代行走過程，這段程式碼執行量子行走的迭代過程：

• 透過 for 迴圈迭代執行steps次（由參數設定）
• 每一步中，使用單步演化算符U作用於當前量子態state
• U @ state 表示矩陣與向量的乘法，實現量子態的演化

第六步計算機率分佈：將量子態向量state重塑為 (2, num_positions)的矩陣，區分硬幣和位置兩個子系統，計算量子振幅的絕對值平方np.abs(...)**2，得到每個狀態的機率，使用 sum(axis=0) 對硬幣維度進行求和，得到僅依賴於位置的邊緣機率分佈，結果 pos_prob 是一個長度為 num_positions 的向量，表示量子行走者在各位置的機率。

 

二、Qiskit 電路版

1. 環境準備
   首先，在 Colab 中執行 !pip install -q qiskit qiskit-aer 來安裝 Qiskit 及 Aer 模擬器，並在程式最上方匯入必要模組：
   

 

2. 定義兩個可重複使用的子電路：加1(incrementor)及減1（decrementor）
   

 

3. 量子行走單步(quantum_walk_step)
   

 

4. 整體模擬(run_dtqw)

• 建立 1 個 coin qubit、n 個位置 qubit 與相同數量的古典暫存器；
• 將位置初始化到畫面中央（或使用者指定的 init_pos）；
• 反覆呼叫 quantum_walk_step 多次以累積演化；
• 最後只量測位置 qubit，透過 AerSimulator 執行並取得測量結果。
  

 

5. 視覺化
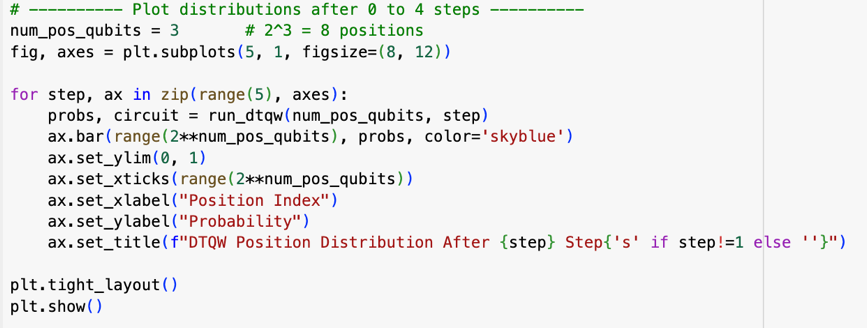
   利用 Matplotlib 畫出 0 至 4 步的長條圖，標示出「位置索引」與「機率」，即可直觀觀察量子行走的多峰與干涉特性。
   

 

最後視覺化結果：這張圖展示了一個離散時間量子行走 (DTQW) 在不同步數下的位置機率分佈。由上至下分別顯示了步數為 0, 1, 2, 3, 4 的情況：

 

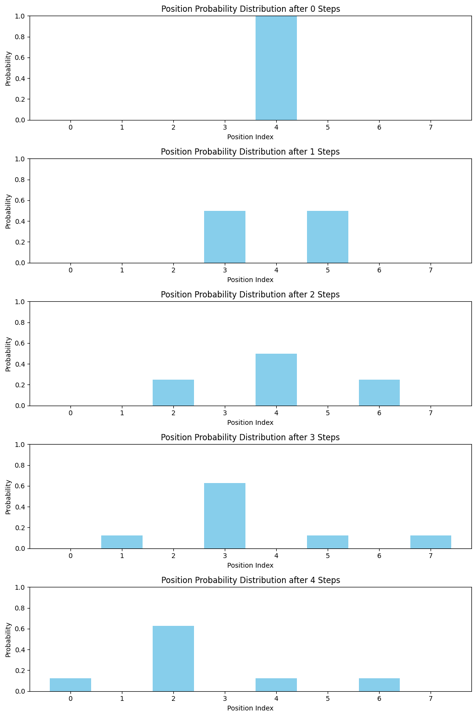
這個演化過程清晰展示了量子行走的獨特性質：由於量子干涉效應，行走者的機率分佈呈現出非高斯特性，擴散速度更快，並且在不同位置形成交替變化的機率峰值。這種行為與經典隨機行走形成鮮明對比，也是量子行走在搜索和傳輸等應用中具有優勢的物理基礎。

 

結語

本文透過兩段程式示範，將量子行走的理論落地到可複現的模擬。NumPy 版讓讀者聚焦於演化矩陣結構，Qiskit 版則提供可直接部署至雲端量子處理器的藍圖。

隨著硬體 qubit 數提升與錯誤率下降，量子行走演算法有望率先在中等規模圖搜尋、特定優化實例上顯現量子優勢。建議讀者在Colab嘗試不同圖形與步數，培養直覺並為更複雜的圖論／金融／機器學習應用奠定基礎。