作者:許達稔、鄭原忠* / *臺灣大學化學系副教授
量子化學方法利用量子力學原理計算原子、分子的各式性質,在化學、物理、材料、光電工程等等領域都有著重要的應用,讓科學家得以利用電腦軟體計算預測許多化學性質,如分子的能量、最佳化結構、振動頻率、光譜、熱化學性質等等,在眾多的計算化學軟體之中,Gaussian應該是最多人使用,而且功能極為強大的一套軟體。我們計畫分四篇文章為您介紹Gaussian的計算執行以及應用。本文是第一篇,將為讀者做最基本的簡介,我們將會介紹執行Gaussian計算的方法,特別是在台大計資中心的高效能叢集電腦系統上面執行Gaussian計算的環境,以及Gaussian輸出的基本資訊解讀。
量子化學計算簡介
化學這一學科,與人類的生活息息相關。自古以來,人們利用身邊取得的材料,燒製陶器、提煉金屬、萃取藥物、製備肥皂、煮食、釀酒,無一不與化學有關。自波義耳及拉瓦節提出元素概念、道爾頓提出原子論、門得列夫提出元素週期表後,化學成為一門研究物性與變化的學科。到了二十世紀,物理界出現量子力學這一分支,海森堡建立了矩陣力學,而薛丁格了建立波動力學。這些理論被應用到化學系統,其名為量子化學。
早期的量子化學應用,侷限在簡單的系統。例如在量子化學課堂中見到的離散能階particle in a box及其延伸應用於有機分子共軛π軌域系統的Huckel theory,進階一些的分子振動模型quantum harmonic oscillator和分子轉動模型rigid rotor等,皆是有解析解的模型。然而,大部分的多體系統都無法以解析解處理,只能以Hartree-Fock等方法做迭代、近似解,以計算多電子分子體系的各式分子性質而言,其計算量極大,以人工根本無法完成,因此一直要到電腦系統問世,才出現通往解答的小徑,而Gaussian軟體的問世,則為量子化學開拓了一條大道。
在眾多的計算化學軟體之中,Gaussian是一個非常受到歡迎而且功能極為強大的軟體,它最早是由約翰.波普爵士(1998年諾貝爾化學獎得主)與他在卡內基梅隆大學的研究團隊發展出的一套程式,這個程式利用高斯函數近似軌域,大幅降低了求解所需的計算量,允許使用者得到以前無法求得的許多結果,因此受到歡迎,很快的便商業化,轉由私人公司經營維護 (http://www.gaussian.com)。Gaussian被廣泛應用在各式化學系統中,計算並預測許多化學性質,如分子的能量、最佳化結構、振動頻率、光譜、熱化學性質等等。Gaussian自1970年推出以來,不斷更新至今,最新版本為Gaussian 09,已經包含齊全的理論計算方法(註1)。Gaussian軟體目前主要應用於Unix-like系統,雖然有推出Windows版本的G09W,卻尚未完全支援64位元系統,也無法達到平行運算效果。Gaussian並非免費軟體,須與該公司購買授權,才能使用;在台灣大學,則可以聯絡計資中心,以高速運算系統應用此軟體。
在這一系列的文章裡面,我們計畫分四篇文章為您介紹Gaussian的計算執行以及應用。本文是第一篇,將為讀者做最基本的簡介,我們將會介紹執行Gaussian計算的方法,特別是在台大計資中心的高效能叢集電腦系統上面執行Gaussian計算的環境,以及Gaussian輸出的基本資訊。接下來的三篇將分別介紹圖形介面的輸入檔製作以及計算結果分析程式、化學反應路徑計算與中間體分析、分子激發態性質計算等等應用。這一系列文章裡,我們將會專注於基於第一原理(first principle, ab initio)的電子結構方法,用來計算分子的性質以及反應特性,由於篇幅的限制,在這一系列文章之中我們將不會談到這些計算的原理以及計算方法的使用範圍與優缺點,這些資訊可以在網路上面找到(註2)。此外,我們也假設讀者已經有基本的叢集系統操作能力,包含在系統上面編輯檔案以及管理排程系統的能力。希望透過這四篇文章,讓就算不是理論化學背景的讀者,也可以利用Gaussian這個工具來解決在研究上面碰到的問題。
進行g09計算
台大計中g09環境簡介
雖然Gaussian是一個非常複雜的程式,而且它應用的理論十分艱深,不過使用Gaussian的邏輯卻十分簡易:只用者只要以Gaussian指定的格式將輸入檔做好,接下來只要執行Gaussian的可執行檔(或由工作主機中的排程系統呼叫Gaussian),計算此輸入檔,再等待輸出即可。目前台大計資中心的叢集電腦上都有支援Gaussian計算,安裝的是Gaussian09的Linux版本,可執行檔是g09。我們以i90叢集為例,g09是安裝在/opt/gaussian的位置,因此使用者在登入後,只要執行下列指令便能使用g09:

執行 g09 時常用 “g09 < jobfile.com > jobfile.log 2>&1” 的指令格式來讀入 jobfile.com 這個檔案裡面的Gaussian指令,並且將計算結果存到jobfile.log這個輸出檔裡面 (註3)。這個語法的計算會在登入的主機上直接進行,只適用於測試輸入檔或是比較小的計算。一般在計算時必須丟到排程系統中,由排程系統在計算節點上呼叫g09 執行,在台大計資中心的 i90 叢集系統上這個過程可以用 /opt/gaussian/rung09 這支程式很簡單地完成,稍後我們會用一個實際的例子來展示這個過程。
g09 輸入檔格式
Gaussian是依據使用者給的輸入檔裡面的指令進行計算,因此在執行 Gaussian計算的時候,準備適當的輸入檔是最重要的工作,在學習使用Gaussian的時候,直接從輸入檔的例子學習重要的語法是最有效的(註4),下面便是一個利用Gaussian計算水分子(見右圖) 性質的輸入檔範例:
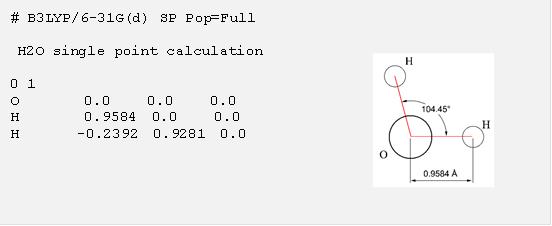
從這個輸入檔裡可以看出一個 Gaussian 計算的輸入檔必須要提供的三項基本資訊:第一行用 “#” 開頭的部分稱之為 route section,這部份使用者以關鍵字指定運算資源需求、使用的理論方法、基底函數 (用以描述分子軌域的一組函數) 、計算的種類以及程式要輸出的資訊等等關於程式控制的要求,在這個範例裡 “B3LYP/6-31G(d)” 表示要用 B3LYP 密度泛函 (DFT) 方法以及 6-31G(d) 這組基底函數進行計算,“SP” 表示要做一個單點計算,“Pop=Full” 則是要 Gaussian 輸出所有軌域相關資料 (預設是印出 10 個前沿軌域),空一行以後的第二個部分是計算的標題,使用者可以填入任何資訊,再空一行以後的第三個部分則描述分子的性質以及所有原子的座標,在這個例子裡面, “0 1” 表示分子是電中性 (電荷為 0) 而且分子的自旋多重性為 1,接下來便是分子的結構,每一行的開頭為原子種類,接著是該原子的 XYZ 座標,預設是以 A 為單位,這個例子裡面指定了水的結構。注意每一個部分後面的空白行是不能省略的,包含最後的一行。
這邊有一個重要的基本觀念,在進行量子化學計算的時候,使用者必須要給定一個理論模型化學 (model chemistry),程式便使用給定的模型化學進行計算,求得使用者所要求的分子性質,而一個理論模型化學包含了兩個部分,第一個是所要使用的計算方法,第二是計算時所要用到的基底函數,如上面的例子裡, B3LYP/6-31G(d) 便是一個常用的模型化學,這個模型裡面 B3LYP 在很多化學問題上都有不錯的表現,而 6-31G(d) 是一個中等大小的基底函數,是個適合作為開始點的組合。簡單的來說,一個理論模型化學決定了要進行計算時所使用的近視方法,而進行理論計算的時候從低階到高階可以選用許多不同的計算方法,考量的重點主要是系統的大小,做比較多近似的低階方法所需使用的計算量比較少,因此使用者可以比較快得到結果,也可以計算較大的分子,但是就得犧牲準確性。較高階的計算需要使用較多的計算機資源,所以只能應用在小分子。此外,還有基底函數的考慮,使用小的基底計算會比較快,然而計算結果一般而言也會較不準確。在進行模擬的時候想要得到正確並且可以信賴的計算結果,化學模型的選擇非常重要,而要選擇適當的模型化學,就需要靠研究者的經驗以及從文獻裡面找尋驗證過的結果了。總而言之,Gaussian運算的效率與正確性,有很高比重取決於使用者的化學智識,視其能否匹配欲計算的化學系統,使用恰當的模型化學而定。以目前的發展,在含有一百個重原子 (不含氫) 大小的分子用 DFT 方法計算基態,已經可以普遍得到接近化學精確度 (誤差 ~ 1 kcal/mol) 的相對能量結果了。
在第一個例子裡面我們用 XYZ 座標輸入分子結構,這有時候不太方便,因此 Gaussian 另外提供了使用 Z-matrix 輸入分子座標的方式,下面便是一個使用 Z-matrix 的例子:

在這個例子裡,分子結構的第一行標示 “O” 是第一個原子,它會被標號為 1 號原子,下一行表示 2 號原子為 “H”,而且它跟 1 號原子的距離為 0.9584 A,接下來 3 號原子為 “H”,它跟 1 號原子的距離為 0.9584 A,而且 ∠3-1-2 為 104.45°,可以清楚看出,這些資訊指定了原子之間的相對座標,可以直接從分子結構中讀出。水只有三個原子,在超過三個原子的系統裡,第四個原子及其以後的所有原子除了標示距離與角度外,還要標示一個兩面角,用以決定一個點在三維空間中真正的位置,後面用到的甲醛例子便有用到兩面角的設定。
執行 g09 計算與檢視計算結果
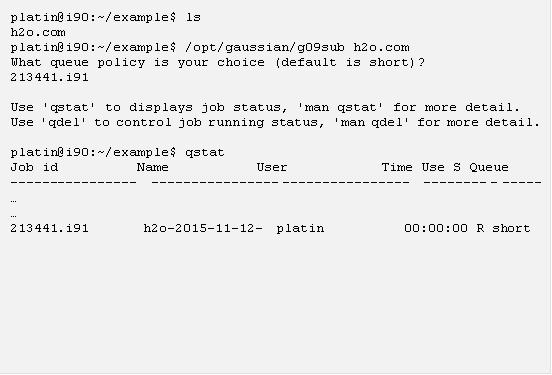
將上面的範例在 i90 上輸入並存成 “h2o.com” 這個輸入檔以後,便可以呼叫 g09 執行計算了,下面的指令便是一個用 g09sub 進行計算的例子:
2. 啟用資料節點服務
sudo /usr/local/mysql/bin/ndbd --initial
執行 g09sub 以後,便可以持續用 qstat 指令檢查,當你沒看到剛剛丟出去的工作時,表示計算跑完了,這時候若用 ls 看一下目前目錄底下的檔案,你會發現 g09sub 幫你用輸入檔的名稱以及目前時間新建了一個目錄,這目錄底下會有一個附加檔名是 .log 的檔案,裡面存有 g09 的計算結果:

現在進入 g09sub 產生的目錄裡面並且看一下輸出檔,例如可以用以下的 less 指令看內容 (請注意你的目錄名稱會因為執行 g09sub 的時間而有所不同):

“h2o.log” 是可以直接閱讀的純文字檔,建議讀者把它從頭到尾看一遍。以下我們列出單點計算裡面比較常用到的資訊,首先找到 “SCF Done:” 開頭的一行:

這一行顯示在完成單點計算以後得到的能量結果,在 E(RB3LYP) 後面的數字便是這個分子在這個結構的單點能量,而能量零點是所有電子與原子核皆完全分離的能量,能量單位是原子單位 (Hartree),一個 Hartree 相當於 627.5 kcal/mol,是相當大的能量 (註 5)。接下來找到描述分子軌域 (MO) 的部分,還可以看到 MO 的相關計算結果:
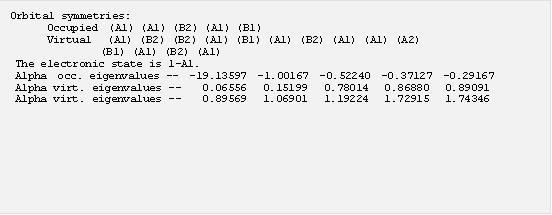
在這個例子裡面,前面五個軌域是填滿電子的 (occupied orbital),後面則是未填電子的軌域 (virtual orbital),因此計算結果水的 HOMO 能量為 -0.19167 A.U. 而 LUMO 能量為 0.06556 A.U.。要注意在密度泛函計算裡面得到的 Kohn-Sham orbital 嚴格來講並不符合 Koopmans’ theorem,因此從 MO 能量預測的游離能並不準確。在這幾行計算結果的後面還有所有 MO 的係數。此外,在單點計算中還可以得到分子內各原子核的電荷分佈,找到 “Mulliken” 開頭的部分:

Gaussian 預設是輸出 Mulliken 的原子電荷分析結果,這個結果顯示水分子中的氧帶部分正電而氫帶部分正電,符合我們的預期。不過,Mulliken 分析方式是純粹從 MO 在基底函數的原子軌域分佈去求得電子的分佈,這樣子的計算雖然直觀但是卻沒有考慮到電子在空間中的分佈情形,因此經常不能妥善的表示原子上的部分電荷性質,應用的時候應該非常小心,Gaussian 因此還提供了更多分析電子分布的方法可以使用 (註6)。最後還有偶極矩相關的計算結果:

這個例子算出水在真空中的偶極矩為 2.08 Debye,實驗值約為 1.85 Debye,B3LYP 在這邊表現比較不好,但是也在 10% 誤差範圍之內了。
分子結構計算
上一節我們用最簡單的單點計算當例子,得到分子在一個固定結構底下的性質。但是更多時候我們並沒有分子的結構,或者想用理論計算方法預測分子的三度空間結構,這個時候我們可以利用 “Opt” 這個關鍵字,要求 g09 進行結構優化的計算,找出一個分子系統的穩定結構。在這個計算中,使用者需要提供一個猜測的初始結構, g09 便會計算出這個結構附近的分子局域穩定結構 (local minimal energy structure)。下面的例子是對甲醛分子 (H2CO) 進行結構優化的計算輸入檔,我們特意用 “%Mem=1GB” 指定每一執行緒使用的記憶體大小為 1GB, “%NProcShare-8” 指定要在單機上用八個執行緒做平行運算,這個設定對甲醛分子是殺雞用牛刀,但是使用者在做比較大分子的計算的時候將會需要設定記憶體及平行運算。初始結構部分我們設定 C=O 鍵長為 1.2 A,C-H 鍵長為 1.1 A,鍵角皆為 120° 的平面分子。
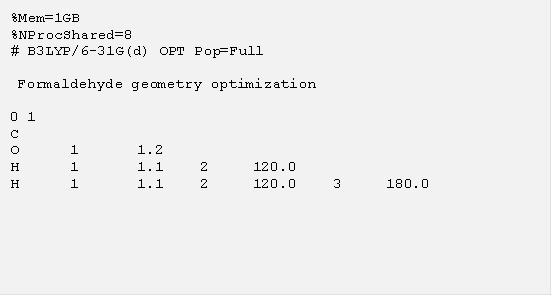
把這個輸入檔存成 h2co.com 並執行計算,在計算結果裡面可以找到 “Optimization completed” 的話表示 g09 成功的找到了穩定的結構,如下:
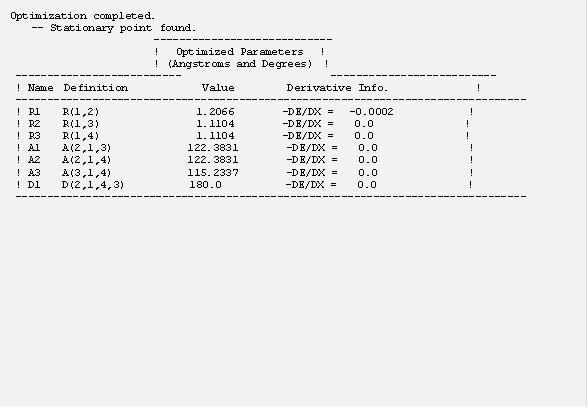
這個計算結果我們得到C=O 鍵長為 1.21 A,C-H 鍵長為 1.11 A,且 ∠H-C-H 約為 115° ,與實驗值非常接近。一般而言, DFT 計算可以給出頗為準確的分子結構。
備註
1. Gaussian 09 的完整功能: http://www.gaussian.com/g_prod/g09_glance.htm
2. 例如,可以參考台大開放式課程中的量子化學課程 (http://ocw.aca.ntu.edu.tw/ntu-ocw/index.php/ocw/cou/101S212),特別是單元 20-23 的部分。
3. 此處使用的檔名並無限制,但是一般習慣 Gaussian 輸入檔用 .com 結尾,輸出檔則用.log。
4. 在 i90 上的 /opt/Gaussian/g09/tests/com 目錄下可以找到 Gaussian 提供的許多範例檔案,是非常有用的學習參考。
5. 關於能量單位轉換可以參考 http://users.mccammon.ucsd.edu/~dzhang/energy-unit-conv-table.html
6. 請參考 http://www.gaussian.com/g_tech/g_ur/k_population.htm